Calculate terms of geometric sequences efficiently. Ideal for mathematical studies and pattern analysis.
The Geometric Sequence Calculator is a powerful tool that allows you to quickly and easily calculate various properties of a geometric sequence. Whether you're a student learning about geometric sequences for the first time or a seasoned mathematician looking to save time on calculations, this calculator is designed to meet your needs.
The general form of a geometric sequence is given by
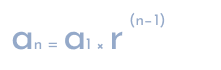
The sum of the first n terms of a geometric sequence can be calculated using the formula, where Sn is the sum of the first n terms.
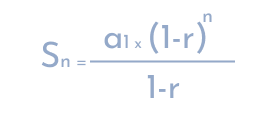
A geometric sequence is a series of numbers where each term is found by multiplying the previous term by a constant value called the common ratio. For example, in the sequence 2, 6, 18, 54, the common ratio is 3 because each term is obtained by multiplying the previous term by 3.
Yes, the calculator can handle geometric sequences with negative terms. It performs the calculations using the same formula, regardless of whether the terms are positive or negative.
A geometric sequence converges if the common ratio is between -1 and 1. This means that as you add more terms to the sequence, the terms get closer and closer to a certain value. If the common ratio is greater than or equal to 1, the sequence diverges, meaning that the terms grow larger and larger without approaching a specific value.
To find the nth term of a geometric sequence using the calculator, you need to enter the first term of the sequence, the common ratio, and the term number (n) into the appropriate fields.