Perform complex quaternion calculations with ease. Ideal for 3D graphics programmers and mathematicians.
A Quaternion Calculator is a tool used for performing mathematical operations involving quaternions. Quaternions are mathematical entities that extend the concept of complex numbers. While complex numbers have two components (real and imaginary parts), quaternions have four components.
The calculator allows users to add, subtract, multiply, and divide quaternions. It can also convert quaternions to other forms, such as Euler angles or rotation matrices.
In various fields like mathematics, physics, and computer graphics, quaternions are used to represent rotations in three-dimensional space. They are particularly useful in computer graphics for smoothly rotating objects without the risk of gimbal lock, a problem that can occur with other rotation representations.
Quaternions play a crucial role in mathematics, particularly in areas involving three-dimensional space and rotations. They offer several advantages and applications that make them an important concept in various fields. Here are some key points highlighting the importance of quaternions in mathematics:
Representation of Rotations: Quaternions provide an efficient way to represent rotations in three-dimensional space. Unlike other methods like Euler angles, quaternions do not suffer from gimbal lock, making them a preferred choice for representing orientations in 3D graphics and robotics.
Simplicity in Rotation Operations: Quaternion multiplication is a simple and effective way to combine multiple rotations. This property makes quaternions valuable in applications where complex rotations need to be calculated efficiently.
Interpolation: Quaternions can be used to interpolate between two orientations smoothly. This property is particularly useful in computer animation and robotics, where smooth transitions between poses are required.
Converting Euler angles to a quaternion involves several steps, depending on the order of rotations (e.g., pitch, yaw, and roll) and the coordinate system used (e.g., XYZ, ZYX).

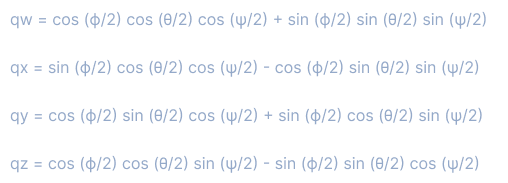
Finally, normalize the quaternion to ensure it has unit length:
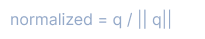
This normalized quaternion represents the same orientation as the given Euler angles.
Quaternions have various applications in real life, ranging from engineering and physics to computer graphics and robotics. Some notable applications include:
Robotics: Quaternions are used to represent the orientation of robotic arms and other mechanical systems. They help calculate the position and orientation of robot end-effectors accurately.
Aerospace Engineering: Quaternions play a crucial role in aerospace applications, such as spacecraft attitude control and navigation. They provide a compact and efficient way to represent complex rotations.
Computer Graphics: In computer graphics, quaternions are used to represent rotations of objects in 3D space. They help achieve smooth and natural-looking animations without gimbal lock issues.
Virtual Reality (VR) and Augmented Reality (AR): Quaternions are used in VR and AR applications to track the orientation of head-mounted displays and other devices. This tracking helps create immersive and realistic experiences.
Animation: In animation, quaternions are used to interpolate between keyframes smoothly. This interpolation ensures that the motion of animated characters and objects appears natural and fluid.
Physics Simulations: Quaternions are used in physics simulations to represent the orientation of rigid bodies. They help simulate realistic movements and interactions between objects in virtual environments.
Navigation Systems: Quaternions are used in navigation systems, such as GPS receivers and inertial navigation systems, to determine the orientation of vehicles and devices accurately.
Medical Imaging: Quaternions are used in medical imaging to represent the orientation of 3D models of anatomical structures. This representation helps in surgical planning and simulation.
Quaternions consist of four components: a scalar part (also known as the real part) and a vector part (composed of three imaginary components). The scalar part represents the rotation angle, while the vector part represents the axis of rotation.
While both quaternions and complex numbers are extensions of real numbers, they differ in their number of components. Complex numbers have two components (a real part and an imaginary part), while quaternions have four components (a scalar part and three imaginary parts).
Gimbal lock occurs when one of the rotational degrees of freedom becomes redundant, leading to a loss of one degree of freedom in describing rotations. Quaternions avoid gimbal lock by representing rotations using a four-dimensional space, which does not suffer from redundancy or locking issues.
No, quaternions are primarily used to represent rotations in three-dimensional space. While they can represent rotations and scales, they do not directly represent translations. Other mathematical constructs, such as translation vectors, are used to represent translations.